Medidas de forma en estadística descriptiva: Representaciones gráficas
Generalidades
Una forma común y efectiva de resumir los valores de las variables, luego de recoger, organizar y cuantificar los datos, es mediante representaciones gráficas. Estas complementan las tablas y ofrecen una forma visual para analizar la información.
Los distintos tipos de gráficos constituyen herramientas indispensables para resumir y comunicar los resultados estadísticos. Estos permiten transmitir información de manera rápida, directa y comprensible, siendo un recurso clave tanto en la presentación de resultados como en el análisis estadístico.
Las representaciones gráficas tienen múltiples ventajas:
- Impacto visual: Llaman la atención del lector.
- Facilidad de lectura: Permiten una interpretación rápida.
- Resumen global: Ofrecen una visión integral de la muestra o población estudiada.
La elección del tipo de gráfico adecuado dependerá del tipo de datos o variables, así como de los objetivos que se persiguen al presentar la información. El carácter de los datos, ya sea cualitativo, cuantitativo discreto o cuantitativo continuo, influye directamente en la selección del gráfico. Incluso dentro de un mismo tipo de dato, ciertos gráficos pueden ser más efectivos para resumir conceptos específicos.
A continuación, se presentan las condiciones que deben cumplir las representaciones gráficas:
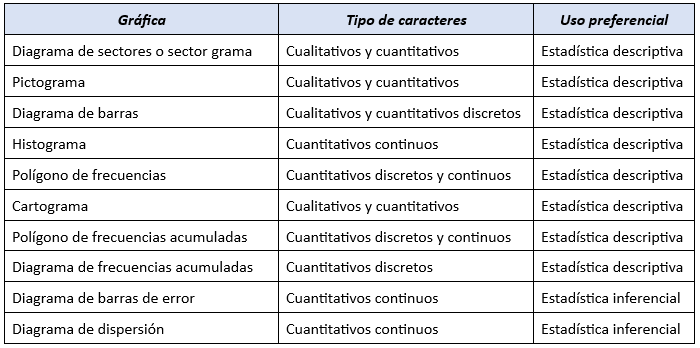
Tipos de representaciones gráficas según el tipo de datos
El tipo de gráfico a emplear dependerá de la naturaleza de los datos. Los gráficos más comunes incluyen:
- Gráficos de barras: Adecuados para variables cualitativas y cuantitativas discretas.
- Histogramas: Indicados para variables cuantitativas continuas.
- Polígonos de frecuencias: Útiles para comparar distribuciones.
- Gráficos circulares: Idóneos para proporciones relativas o porcentajes.
- Diagramas de dispersión: Representan relaciones entre dos variables cuantitativas.
Histograma
El histograma es un tipo de gráfico que se utiliza principalmente para representar datos cuantitativos agrupados en intervalos de clase. Aunque su uso principal es para este tipo de datos, también puede emplearse para presentar otras modalidades de información. En este gráfico, la figura básica que se utiliza es el rectángulo.
Para construir un histograma, se utiliza un sistema de ejes coordenados, donde se representan los siguientes elementos:
1. Eje de abscisas (horizontal):
En este eje se colocan los intervalos de clase (Xi), que corresponden a las divisiones del rango de valores del conjunto de datos.
2. Eje de ordenadas (vertical):
En este eje se representa la frecuencia (ni, fi o porcentaje) de los datos. La altura de cada rectángulo es proporcional a la frecuencia del intervalo correspondiente.
Representación según el tipo de datos:
- Datos discretos o cualitativos:
Los rectángulos no estarán adosados, es decir, habrá espacios entre ellos, ya que los valores no forman un continuo. - Datos continuos (intervalos de clase):
En este caso, los rectángulos estarán adosados, ya que los intervalos de clase son contiguos y no hay espacios entre ellos. Cada rectángulo tendrá como base el segmento que corresponde al intervalo, y la altura del rectángulo será proporcional a la frecuencia absoluta (fi) o a la frecuencia relativa (hi = fi/N).
Área de los rectángulos:
El área de cada rectángulo en un histograma es proporcional a la frecuencia del intervalo que representa. Por lo tanto, el área de un rectángulo es:
Area = base × altura
Donde:
- La base corresponde a la amplitud del intervalo.
- La altura depende de la frecuencia absoluta o relativa.
El histograma es especialmente útil para visualizar la distribución de datos en una variable continua, identificar tendencias, y observar patrones como la simetría, asimetría, o la concentración de valores en determinados rangos.
Representación de intervalos de clase con amplitudes diferentes
En ocasiones, es necesario trabajar con intervalos de clase que tienen distintas amplitudes. Para representarlos correctamente, se elige una amplitud como referencia, generalmente la menor, y se determinan las alturas correspondientes a cada intervalo siguiendo la ecuación:
Frecuencia (área) = amplitud del intervalo × altura
En algunos estudios, puede ocurrir que las frecuencias sean muy pequeñas, lo que daría lugar a gráficos con alturas demasiado bajas y poca claridad visual. Para resolver esto, se opta por multiplicar todas las frecuencias por un mismo factor, haciendo que sean proporcionales entre sí y mejorando la visualización. En estos casos, es fundamental advertir de esta operación en el título o enunciado del gráfico.
Polígonos de frecuencias
Los polígonos de frecuencias son gráficos lineales utilizados para representar datos cuantitativos (y en ocasiones ordinales). Se construyen sobre un eje de coordenadas en el que se colocan las clases de datos y sus respectivas frecuencias. Los puntos obtenidos al cruzar esta información se unen mediante segmentos de recta, formando una línea quebrada. Esta línea pasa por los puntos medios de los extremos superiores de los rectángulos del histograma o de las barras del diagrama de barras.
Existe una variante llamada polígono de frecuencias acumuladas, que sirve para representar distribuciones acumuladas, ya sean absolutas o relativas. Este gráfico une, mediante segmentos, los puntos correspondientes a los extremos superiores de cada intervalo, representando la frecuencia acumulada. Este tipo de polígono se adapta tanto a intervalos de igual como de distinta amplitud.
Además, se pueden realizar polígonos comparativos para analizar dos distribuciones o series estadísticas que tengan un mismo significado.
Por último, es posible combinar en un mismo gráfico el histograma de una muestra y su polígono de frecuencias, ofreciendo una visión más completa de los datos.
Diagramas de barras
Los diagramas de barras son similares al histograma, pero utilizan barras separadas en lugar de rectángulos adyacentes. Son especialmente útiles para representar caracteres cualitativos, cuasicuantitativos o cuantitativos discretos en los que la variable toma pocos valores.
Según la orientación del gráfico, se clasifican en:
1. Diagramas de barras verticales: Los valores de la variable se colocan en el eje horizontal (abscisas), mientras que las frecuencias (absolutas, relativas o porcentuales) se representan en el eje vertical (ordenadas).
2. Diagramas de barras horizontales: Los valores de la variable se sitúan en el eje vertical, mientras que las frecuencias se representan en el eje horizontal.
Para su construcción, se dibujan tantas barras como categorías existan en el carácter cualitativo estudiado, o tantos valores como tome la variable en los casos cuantitativos discretos.
Además, se pueden realizar gráficos tridimensionales, añadiendo un tercer eje que permite representar prismas rectangulares en lugar de barras simples, ofreciendo una perspectiva más visual y detallada.
Pictogramas
Los pictogramas son gráficos en los que se utiliza un dibujo o figura para representar las frecuencias de una variable. Hay varias maneras de elaborarlos, pero destacan dos principales:
1. Pictogramas de repetición: Se asigna un valor al dibujo en función de la frecuencia, repitiendo la figura tantas veces como sea necesario según la cantidad que representa cada modalidad de la variable.
2. Pictogramas de amplificación: A cada clase se le asigna una figura distinta cuya área es proporcional a la frecuencia correspondiente.
Sectorgramas o diagramas de sectores
Los sectorgramas, también llamados diagramas de sectores, son gráficos circulares en los que cada clase o modalidad de la variable se representa mediante un sector proporcional a su frecuencia (similar a las porciones de una tarta).
Se utilizan principalmente para representar datos cualitativos, cuasicuantitativos o cuantitativos discretos no agrupados que toman pocos valores. Son especialmente útiles cuando se desea resaltar las proporciones de ciertos subconjuntos en relación con el total.
El procedimiento para construir un diagrama de sectores parte del hecho de que el área total del círculo corresponde a 360°. Se divide en sectores circulares según el número de clases o modalidades, asignando a cada uno un ángulo proporcional a la frecuencia absoluta o relativa, utilizando la fórmula:
X = fi × 360
Donde fi representa la frecuencia de la categoría.
Cada sector incluye información sobre el número de casos en cada categoría y el porcentaje que estos representan respecto al total.
Sin embargo, si hay demasiadas categorías, el gráfico puede volverse confuso y poco claro. Del mismo modo, cuando algunas categorías tienen frecuencias muy bajas, puede ser difícil representarlas e interpretarlas adecuadamente.
Cartogramas
Los cartogramas son gráficos que representan una región o área geográfica, destacando una variable específica relacionada con dicha zona. Por ejemplo, se podrían usar para mostrar la densidad de población en diferentes provincias de Galicia.
Las categorías de la variable se distinguen según su frecuencia, utilizando diferentes estilos, como trazos variados o colores distintos, para facilitar su diferenciación.
Otras medidas de forma
Además de los gráficos mencionados anteriormente, existen otras formas de representación utilizadas en estadística descriptiva, aunque las descritas son las más importantes.
Asimismo, hay gráficos que son característicos de la estadística inferencial, como el diagrama de barras de error o el diagrama de dispersión (usado en análisis de correlación), los cuales no se abordan en esta unidad.


