6. Relaciones entre variables: correlación y regresión. TEMA 10 TÉCNICO DE LABORATORIO SESCAM

Relaciones entre Variables: Correlación y Regresión

En estudios estadísticos, a menudo se busca analizar dos o más características de una población que están relacionadas entre sí. Por ejemplo, la altura, el peso y la edad de un grupo de individuos. En este contexto, resulta esencial comprender las relaciones entre las variables para interpretar mejor los datos.

Variables Estadísticas Bidimensionales

Cuando estudiamos dos variables juntas, estas se denominan variables estadísticas bidimensionales. Cada observación se representa mediante un par ordenado (x,y)(x, y)(x,y), donde:

• x: valor de la primera variable.
• y: valor de la segunda variable.

Por ejemplo, al estudiar la altura y el peso de un grupo de 10 personas, se podrían obtener pares como:
(165, 58),(165, 62),(168, 67),(171, 66),(173, 65),(180, 78),(157, 63),(162, 57),(180, 82),(175, 80)(165, 58), (165, 62), (168, 67), (171, 66), (173, 65), (180, 78), (157, 63), (162, 57), (180, 82), (175, 80)(165, 58),(165, 62),(168, 67),(171, 66),(173, 65),(180, 78),(157, 63),(162, 57),(180, 82),(175, 80).

Distribuciones Conjuntas y Marginales

a) Distribución conjunta de frecuencias

Frecuencia absoluta (n_ij​):
Es el número de veces que aparece un par (x_i, y_j) en los datos.

Frecuencia relativa (f_ij​):
Es el cociente entre la frecuencia absoluta de un par (x_i, y_j) y el número total de observaciones (N):

f_ij = n_ij / N

b) Distribuciones marginales de frecuencias

Distribución marginal de la variable X:
Considera los valores de x₁, x₂, …, x_i, x_k y sus frecuencias absolutas (n₁, n₂,…, n_k), independientemente de los valores de Y.

Distribución marginal de la variable Y:
Incluye los valores de y1, y₂,…,y_p​ y sus frecuencias absolutas (n₁, n₂,…, n_p), independientemente de los valores de X.

Frecuencia relativa marginal:
Es la frecuencia relativa de los pares cuyo primer elemento es x_i​, independientemente del segundo valor y₁,

f_xi = Suma de n_ij para todos los j / N

​De forma similar, se define la frecuencia relativa marginal para Y:

f_yj = Suma de n_ij para todos los i / N

Correlación

La correlación mide la intensidad y dirección de la relación lineal entre dos variables cuantitativas. Se utiliza el coeficiente de correlación de Pearson (r), cuya fórmula es:

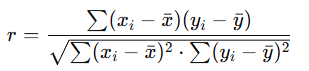
• r toma valores entre −1 y 1:
• r > 0: Relación positiva (a mayor x, mayor y).
• r < 0: Relación negativa (a mayor x, menor y).
• r = 0: No hay relación lineal.

Regresión

La regresión permite predecir el valor de una variable (Y) en función de otra (X). La ecuación de la regresión lineal es:

y = a + bx

Donde:

• a: Intersección con el eje Y (ordenada al origen).
• b: Pendiente de la línea, que indica el cambio en Y por cada unidad de cambio en X.

Cálculo de a y b:

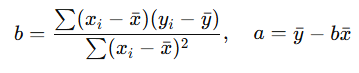
Aplicaciones

Correlación: Determina si existe una relación entre dos variables y la dirección de esta relación.

Regresión: Predice valores de Y a partir de X, siendo especialmente útil en modelos predictivos y análisis de tendencias.

La frecuencia relativa marginal de Y_j se refiere a la proporción de observaciones en las que el segundo elemento de los pares de datos es Y_j​, sin importar el valor del primer elemento (X_i).

Se representa como f_.j y su fórmula es:

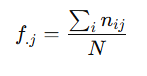
Donde:

• n_ij​: Frecuencia absoluta de observaciones correspondientes al par (X_i, Y_j).
• ∑_i n_ij​: Suma de las frecuencias absolutas de todas las combinaciones de X_i​ con Y_j​.
• N: Total de observaciones en la muestra.

En otras palabras, es el cociente entre el total de observaciones para el valor Y_j​ y el tamaño total de la muestra.

Tablas Bidimensionales

Las tablas bidimensionales se utilizan para mostrar de manera tabular la relación entre dos variables cuantitativas. Estas tablas se organizan como una estructura de doble entrada.

Construcción de una tabla bidimensional

1. Ejes de la tabla:

• Filas: En la primera columna se colocan los valores de la variable X.
• Columnas: En la primera fila se colocan los valores de la variable Y.

2. Frecuencias absolutas (n_ij​):

• En cada celda de la tabla, se coloca la frecuencia absoluta (n_ij​) correspondiente al par de valores (x_i,y_j).
• Esto representa el número de veces que la combinación de valores x_i​ y y_j aparece en los datos.

3. Totales:

• Totales por filas: En la última columna se colocan las sumas de las frecuencias absolutas de cada fila (∑_j n_ij).
• Totales por columnas: En la última fila se colocan las sumas de las frecuencias absolutas de cada columna (∑_i n_ij).
• Frecuencia absoluta conjunta: En la esquina inferior derecha de la tabla se coloca el total general (∑_i ∑_j n_ij = N).

4. Distribuciones marginales:

• La distribución marginal de X se obtiene de la primera y última columna de la tabla.
• La distribución marginal de Y se obtiene de la primera y última fila de la tabla.

Variantes con frecuencias relativas

En lugar de utilizar las frecuencias absolutas (n_ij), se pueden usar las frecuencias relativas (f_ij​).

• Cada celda contendrá f_ij = n_ij / N​​.
• En este caso, el total general de las frecuencias relativas será igual a 1.

Diagrama de Dispersión

El diagrama de dispersión es una representación gráfica que muestra la relación entre dos variables cuantitativas. Consiste en un conjunto de puntos en un sistema de ejes de coordenadas, donde cada punto representa los valores de las dos variables para un individuo.

Construcción de un diagrama de dispersión

1. Ejes de coordenadas:
   • Eje horizontal (abscisas): Se representan los valores de la variable X.
   • Eje vertical (ordenadas): Se representan los valores de la variable Y.
2. Representación de puntos:
   • Cada par de valores (x_i, y_j) se representa como un punto en el plano.
   • Si se utiliza la frecuencia absoluta asociada a (x_i, y_j), se puede dibujar un círculo proporcional a esa frecuencia alrededor del punto.

Tipos de relaciones en un diagrama de dispersión

1. Relación directa:
   • Ambas variables aumentan o disminuyen juntas.
   • Ejemplo: Si X crece, Y también crece; y si X disminuye, Y también disminuye.
2. Relación inversa:
   • Una variable aumenta mientras la otra disminuye.
   • Ejemplo: Si X crece, Ydisminuye; y si X disminuye, Y crece.
3. Relación nula:
   • No hay conexión visible entre las variables. Conocer el valor de una no aporta información sobre la otra.
   • En algunos casos, puede existir una relación pero no es evidente en el gráfico debido a errores o patrones no lineales.

Otras representaciones gráficas

Además del diagrama de dispersión, existen gráficos similares a los utilizados para variables unidimensionales. La diferencia es que ahora estas representaciones ocupan el espacio bidimensional, en lugar del plano lineal.

Síntesis de Datos: Covarianza

Las distribuciones marginales de variables bidimensionales tienen los mismos parámetros estadísticos que las variables unidimensionales, como se ha mencionado anteriormente. Sin embargo, al considerar la distribución conjunta de las variables, surge un nuevo parámetro estadístico importante: la covarianza.

Covarianza

La covarianza mide la relación entre dos variables bidimensionales. Es útil para entender tanto la centralización como la dispersión de los datos y se utiliza como base para calcular otros parámetros, como el coeficiente de correlación. La covarianza se denota por S_XY​ o cov (X, Y).

Fórmula de la covarianza:

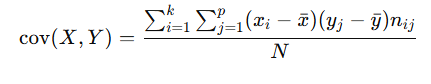
Donde:

x_i​ y y_j​: Valores de las variables X e Y.

n_ij​: Frecuencia absoluta conjunta del par (x_i, y_j).

N: Total de observaciones.

Interpretación de la covarianza:

• S_XY > 0: Relación directa entre las variables (a medida que una aumenta, la otra también).
• S_XY < 0: Relación inversa entre las variables (a medida que una aumenta, la otra disminuye).
• S_XY = 0: Relación nula. Las variables son independientes.

Regresión

La regresión es una herramienta estadística que analiza la relación entre variables cuantitativas. Su principal utilidad es predecir o estimar el valor de una variable dependiente (Y) con base en el valor de una variable independiente (X).

La regresión busca determinar una función matemática que describa de la mejor manera posible la relación entre ambas variables. Esta función se representa gráficamente mediante una línea de regresión.

Tipos de relaciones entre variables cuantitativas:

1. Relación funcional:
Existe una relación exacta entre las variables, definida por una fórmula matemática precisa. Por ejemplo: y = 3x.

2. Relación estadística:
No hay una relación exacta, pero existe una dependencia aproximada que sigue un patrón. En estos casos, se utiliza el análisis de regresión para describir esta relación.

Análisis de regresión

Pasos principales:

1. Representación gráfica:
   • Se construye un diagrama de dispersión con los datos observados.
   • Cada punto del gráfico representa un par (x_i, y_j).
2. Identificación de las variables:
   • X: Variable explicativa o independiente.
   • Y: Variable dependiente o explicada.
3. Observación del patrón:
   • Si los puntos se agrupan alrededor de una línea (recta o curva), es posible modelar la relación con una función matemática, llamada línea de regresión.
4. Obtención de la función matemática:
   • Se determina la ecuación que mejor describe la relación entre X e Y.
   • La forma más común es la regresión lineal, cuya ecuación es:
   • y = a + bx Donde:
     • a: Intersección con el eje Y (ordenada al origen).
     • b: Pendiente de la línea, que representa el cambio en Y por cada unidad de cambio en X.

Ejemplo práctico:

Si estudiamos la relación entre la altura (X) y el peso (Y) de un grupo de personas, es razonable asumir que a mayor altura, mayor peso. En este caso:

• X = Altura (variable independiente).
• Y = Peso (variable dependiente).

Mediante el análisis de regresión, se puede predecir el peso aproximado de una persona dado su valor de altura, estableciendo una relación funcional o estadística entre ambas variables.

Este enfoque proporciona una base para entender y predecir relaciones en datos cuantitativos, siendo fundamental en áreas como la estadística aplicada y la investigación científica.

Regresión Lineal

La regresión lineal es una fórmula matemática que relaciona dos variables cuantitativas mediante una ecuación lineal o recta: Y = a + bX

Donde:

• X: Variable independiente o explicativa.
• Y: Variable dependiente o explicada.
• a y b: Constantes que definen la relación entre las variables y deben calcularse.

Componentes de la ecuación:

a: Representa el punto donde la recta intersecta el eje Y, conocido como la ordenada en el origen.

b: Es la pendiente de la recta, que indica la inclinación y describe cómo cambia Y por cada unidad de cambio en X.

Recta de Regresión

La recta de regresión es aquella que se ajusta mejor al diagrama de dispersión de datos, minimizando las diferencias entre los valores observados y los valores predichos. Este ajuste minimiza los errores de predicción o residuos.

Residuo:

• Definición:
  La diferencia entre el valor observado de Y (y) y el valor predicho por la recta (y′). Residuo (e) = y − y′
• Importancia: Indica qué tan cerca está el valor observado del valor estimado por la recta. Cuanto más pequeño sea el residuo, mejor es el ajuste.

Valores observados y predichos:

• Cada valor de X tiene un y asociado (valor observado) y un y′ (valor predicho), calculado a partir de la ecuación de la recta: y′ = a + bX

Método de los Mínimos Cuadrados

El método de los mínimos cuadrados se utiliza para encontrar los valores de aaa y bbb que minimizan la suma de los cuadrados de los residuos. Es decir, se busca reducir al mínimo la expresión:

∑( y − y′)²

Donde y′ es el valor estimado por la ecuación de la recta.

Procedimiento:

1. Sustituimos y′ = a + bX en la expresión: ∑( y − a − bX)²
2. Utilizando técnicas matemáticas, se derivan las fórmulas para calcular a y b.

Cálculo de b (pendiente):

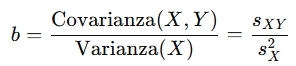
Donde:

• s_XY​: Covarianza entre X e Y.
• s_X²: Varianza de X.

Cálculo de a (ordenada en el origen):

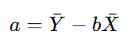
Donde:

Sustitución en la ecuación:

Una vez calculados aaa y bbb, la ecuación de la recta de regresión queda definida como: Y = a + bX

O también puede expresarse de forma centrada:

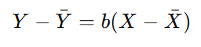
Resumen:

La regresión lineal permite modelar la relación entre dos variables cuantitativas mediante una recta que se ajusta al conjunto de datos. A través del método de los mínimos cuadrados, se minimizan los errores de predicción, proporcionando una herramienta para interpretar y predecir relaciones en datos cuantitativos.

Calidad del Ajuste y Coeficiente de Determinación

Cuando se estudia la relación entre dos variables, la variable independiente (X) no explica completamente todos los valores observados en la variable dependiente (Y). Esto solo sucede si existe una relación funcional perfecta y todos los puntos de la nube de datos se encuentran exactamente sobre la recta de regresión.

Para medir qué tan bien explica X los valores de Y, se utiliza el coeficiente de determinación (R²), que evalúa la calidad del ajuste de la recta de regresión a los datos.

Coeficiente de Determinación

El coeficiente de determinación es un valor numérico que mide cuánto de la variabilidad de Y es explicado por X. También se conoce como la calidad del ajuste, ya que evalúa la cercanía de los puntos de datos a la recta de regresión.

Fórmula:

La varianza de Y puede descomponerse en dos partes:

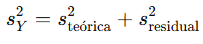
Donde:

• s_Y²​: Varianza total de los datos observados de Y.
• s_teórica²​: Varianza explicada por X, asociada a la recta de regresión.
• s_residual²​: Varianza residual, no explicada por X.

El coeficiente de determinación (R²) se calcula como:

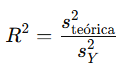
Interpretación:

• R² = 1: Todos los puntos están sobre la recta; el modelo explica completamente la variabilidad de Y.
• R² = 0: No hay relación entre X e Y; la recta no explica ninguna parte de la variabilidad.
• 0 < R² < 1: La recta explica una proporción de la variabilidad de Y, pero no toda.

Recomendación:

Un valor de R² mayor o igual a 0.75 indica un buen ajuste de la recta a los datos observados.

Ejemplo:

Con los valores de un conjunto de datos sobre altura (X) y peso (Y), se calculan:

• Media de X = 169.6, s_X = 7.2139.
• Media de Y = 67.8, s_Y = 8.7567.
• Covarianza entre X e Y = 52.32.

La ecuación de la recta de regresión es:

Y = −102.71 + 1.005X

El coeficiente de determinación es:

R² = 0.6859

Esto indica que aproximadamente el 68.59% de la variabilidad del peso (Y) es explicada por la altura (X).

Correlación

La correlación mide el grado de relación entre dos variables cuantitativas, indicando cuánto varían conjuntamente. En esencia, evalúa qué tan bien describe la línea de regresión la relación entre las variables.

Tipos de correlación:

1. Independencia:
   • No hay relación entre X e Y.
   • Los puntos del diagrama de dispersión están distribuidos aleatoriamente, sin un patrón claro.
2. Correlación perfecta:
   • Existe una relación exacta entre las variables.
   • Los puntos del diagrama de dispersión están exactamente sobre la línea de regresión.
   • Ejemplo: Para un móvil que se desplaza a velocidad constante (v), la relación entre distancia recorrida (e) y tiempo (t) es funcional: e = vt.
3. Correlación lineal:
   • Los puntos del diagrama de dispersión están cerca de una línea recta, que puede ser creciente o decreciente.
   • Correlación positiva:
     • Al aumentar X, también aumenta Y.
     • La línea de regresión es ascendente.
   • Correlación negativa:
     • Al aumentar X, Y disminuye.
     • La línea de regresión es descendente.

Resumen:

• El coeficiente de determinación (R²) mide qué porcentaje de la variabilidad de Y es explicado por X.
• La correlación evalúa la intensidad y dirección de la relación entre las variables.
• Una correlación lineal fuerte sugiere que los puntos están cerca de la línea de regresión, mientras que una débil indica dispersión significativa alrededor de la línea.

Coeficiente de Correlación Lineal

Aunque el diagrama de dispersión brinda una perspectiva cualitativa sobre el tipo de relación entre dos variables, el coeficiente de correlación lineal (r) permite medir cuantitativamente el grado de relación entre variables cuantitativas.

El coeficiente de correlación es un valor numérico que indica el nivel de dependencia entre las variables y qué tan bien se relacionan. Se calcula como el cociente entre la covarianza de las variables y el producto de sus desviaciones típicas:

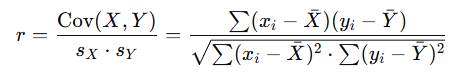
Donde:

• −1 ≤ r ≤ 1.
• s_X​ y s_Y​: Desviaciones típicas de X e Y, respectivamente.
• Cov(X, Y): Covarianza entre las variables X e Y.

Interpretación de r:

1. r = −1:
Existe una relación lineal inversa y perfecta entre las variables. Todos los puntos del diagrama de dispersión están exactamente sobre una recta decreciente.

2. r = 1:
Existe una relación lineal directa y perfecta entre las variables. Todos los puntos están sobre una recta ascendente.

3. r = 0:
No hay relación lineal entre las variables; estas son independientes y no correlacionadas.

4. −1 < r < 0 :
Existe una relación inversa entre las variables. La relación es más fuerte cuanto más cercano sea r a −1.

5. 0 < r < 1:
Existe una relación directa entre las variables. La relación es más fuerte cuanto más cercano esté r a 1.

Notas importantes:

• Valores de r cercanos a 1: indican una relación directa fuerte.
• Valores de r cercanos a −1: indican una relación inversa fuerte.
• Valores de r cercanos a 0: indican una relación lineal débil.

Relación con el coeficiente de determinación:

El coeficiente de determinación (R²) es el cuadrado del coeficiente de correlación lineal:

R² = r²

Representa el porcentaje de variabilidad de Y que puede ser explicado por X.

Aplicación práctica

En el ejemplo anterior sobre Altura (X) y Peso (Y), los datos calculados son:

• r = 0.8282: Lo que indica una relación directa moderadamente fuerte.
• R² = r² = 0.6859: Lo que significa que el 68.59% de la variabilidad en el peso es explicada por la altura.

La relación no es débil, pero tampoco se considera excelente, ya que no toda la variabilidad está explicada por la recta de regresión.

Correlación No Lineal

Cuando R² es cercano a 0, puede que las variables no tengan una relación lineal, pero sí una relación de otro tipo. En estos casos, la nube de puntos no se ajusta a una recta, sino a otras formas geométricas como parábolas, hipérbolas o curvas exponenciales. Para analizar estas relaciones, se utilizan modelos alternativos como:

• Relación exponencial.
• Relación logarítmica.
• Relación potencial.

Transformaciones Linealizables

Existen relaciones no lineales que pueden convertirse en lineales mediante transformaciones matemáticas. Por ejemplo:

• Si las variables están relacionadas por y = axⁿ, al aplicar logaritmos se obtiene:

log ⁡y = n log ⁡x + log⁡ a

Llamando Y = log ⁡y, X = log ⁡x, y A = log ⁡a, la ecuación se transforma en:

Y = A + nX

Esta es una relación lineal entre las nuevas variables transformadas.

Conclusión

El coeficiente de correlación lineal (r) es una herramienta fundamental para medir el grado y la dirección de la relación entre dos variables cuantitativas. Si la relación no es lineal, pueden aplicarse transformaciones para analizarla mediante modelos alternativos o linealizables.