2. Estadística descriptiva: tratamiento de la información recogida y observada. TEMA 10 TÉCNICO DE LABORATORIO SESCAM

Variables

Conceptos generales
Una variable es cualquier magnitud que puede adoptar distintos valores. Por ejemplo:

• Una variable N (número de páginas de un libro) puede tener valores como 50, 100 o 200.
• Una variable T (temperatura en grados centígrados) puede tomar valores como 35 °C, 40 °C, etc.
• Una variable P (un punto en un plano) puede representarse por dos números, como (2,1) o (3,2).

En el ámbito estadístico, se entiende por variable a cualquier atributo o dato que representa a los elementos de una población o muestra. Estas variables pueden ser iguales o diferentes y pueden describir características como la edad, el sexo, los ingresos económicos, o el color del cabello, entre otros.

El incremento de una variable (x) se refiere a la diferencia entre dos de sus valores. Por ejemplo, si el peso de un recién nacido es de 3,5 kg y después de una semana es de 4 kg, el incremento sería de 0,5 kg (4 – 3,5). En caso de que el valor disminuya, se hablará de un decremento.

Tipos de variables

Las variables que caracterizan a una muestra o población pueden clasificarse según diferentes criterios:

A) Según su dependencia:

1. Variable dependiente: sus valores están determinados por otra u otras variables.

2. Variable independiente: determina los valores de la variable dependiente.

Cuando una variable depende de otra u otras, se habla de una función. Por ejemplo:

• Si z depende de x e y, se expresará como z = F (x, y).
• Si y depende solo de x, se expresará como y = F (x) .

B) Según su aleatoriedad:

1. Variable aleatoria: es una función que puede tomar distintos valores numéricos dependiendo de un fenómeno que ocurre de manera aleatoria, es decir, con diferentes probabilidades.

2. Variable no aleatoria: es una función cuyos valores son determinados de forma predecible por un fenómeno determinista, donde los resultados siempre son los mismos.

En estadística se estudian principalmente las variables aleatorias, ya que permiten analizar datos cuyos resultados varían entre individuos, facilitando así predicciones más precisas sobre fenómenos inciertos. La diversidad en los datos aporta más información que la homogeneidad.

C) Según las características o información que recogen

Las variables pueden clasificarse en tres categorías según el tipo de información que representan:

• Variables unidimensionales: Estas variables recogen información sobre una sola característica de los sujetos estudiados. Por ejemplo, el color de cabello de los estudiantes de una clase.

• Variables bidimensionales: Este tipo de variables incluye información sobre dos características de la población en estudio. Por ejemplo, el grupo sanguíneo ABO y el factor Rh de una comunidad específica de personas.

• Variables pluridimensionales: En este caso, se recopilan múltiples datos de la muestra o población en estudio. Un ejemplo sería el grupo sanguíneo ABO, el factor Rh, el hematocrito y la tensión arterial de un grupo particular de personas.

D) Según su significado o naturaleza

Las variables también pueden dividirse en dos tipos según la forma en que describen las características de los sujetos:

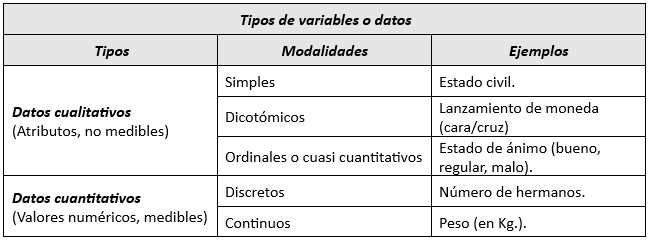
• Variables cualitativas: Estas variables representan atributos o características que no pueden medirse numéricamente. Por ejemplo, el color de cabello de un grupo de personas (negro, castaño, rubio o pelirrojo).

• Variables cuantitativas: Son aquellas que requieren una representación numérica y, por tanto, son medibles. Un ejemplo sería la edad de los sujetos, expresada en años.

Ambos tipos de variables tienen variantes específicas:

a) Variantes de datos cualitativos

• Datos cualitativos dicotómicos: Estas variables solo pueden tener dos valores posibles. Por ejemplo, si un grupo de personas sangra o no tras una inyección intramuscular, o si las personas de la muestra son hombres o mujeres.

• Datos cualitativos ordinales o cuasicuantitativos: Estas variables tienen un orden lógico, ya sea ascendente o descendente. Por ejemplo, el grado de dolor de cabeza que pueden experimentar los sujetos, clasificado como nulo, leve, moderado o intenso.

Las variables cualitativas que no se pueden ordenar se denominan datos cualitativos nominales, como el estado civil (soltero, casado, divorciado, viudo o separado) o el color de cabello (castaño, rubio, moreno o pelirrojo).

b) Variantes de datos cuantitativos

• Datos cuantitativos discretos: Estas variables solo pueden tomar valores específicos y no tienen valores intermedios entre ellos. Por ejemplo, el número de fallecimientos en una ciudad (85 en 2005 y 86 en 2006) no puede promediarse como 85,5 porque no hay medio fallecimiento. Otros ejemplos incluyen el número de hijos, el recuento de leucocitos por 100 ml o el número de bacterias en un coprocultivo.

• Datos cuantitativos continuos: Estas variables pueden tomar cualquier valor dentro de un rango. Por ejemplo, la altura de los individuos de una muestra expresada en centímetros. Entre 170 cm y 171 cm, pueden existir valores intermedios como 170,1 cm, 170,2 cm, etc.

Es importante tener en cuenta que los datos continuos están sujetos a posibles errores de medición, lo que puede convertirlos en datos discretos. Sin embargo, los datos continuos pueden agruparse en intervalos de clase, permitiendo cuantificar los valores que caen dentro de cada intervalo. De manera similar, algunos datos discretos también pueden organizarse en intervalos de clase para facilitar su análisis.

Resumen de datos o variables

Después de recopilar, organizar y clasificar los datos de una muestra o población, es necesario resumirlos para facilitar su análisis. Esto se hace mediante el cálculo de estadísticas o parámetros como la media, la varianza, entre otros. Si la muestra es representativa de la población, los resultados obtenidos pueden usarse para realizar predicciones (inferencia).

Existen dos maneras principales de resumir o presentar los datos:

1. Tabulación: Representar la información en tablas.

2. Gráficos: Mostrar los datos mediante representaciones gráficas.

Un estadístico se define como una función de los valores numéricos de una muestra, por lo que su valor puede variar dependiendo de los datos de la muestra y está sujeto a error. Por otro lado, un parámetro es una función de los valores numéricos de una población, siendo el estadístico una estimación de dicho parámetro.

Distribución de frecuencias

Tipos de frecuencias

Para organizar y representar los datos en tablas, gráficos o para calcular otras medidas como las de posición o dispersión, es esencial ordenarlos a través de una distribución de frecuencias. Esto permite estructurar la información y facilitar su interpretación.

Se define frecuencia como el número de veces que se repite una clase o categoría de una variable en una muestra o población.

Ejemplo:
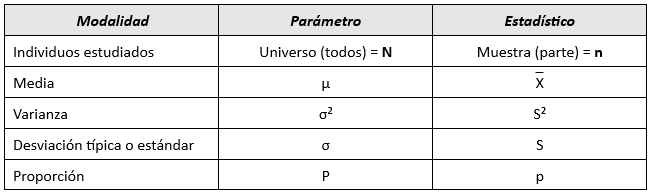
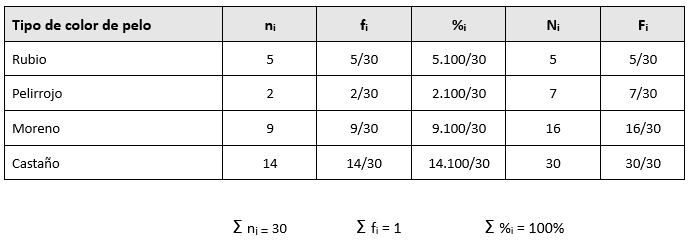
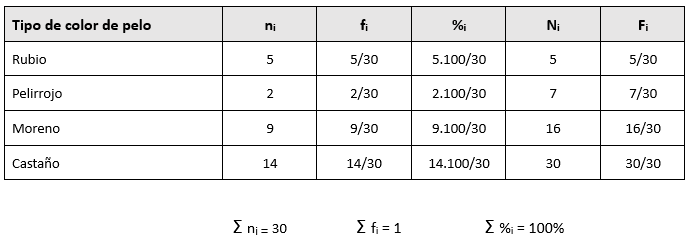
Si tomamos una muestra de 30 estudiantes de un curso superior de documentación sanitaria, y la variable a analizar es el color de cabello, los valores podrían ser:

• Rubio (R): 5 estudiantes.
• Pelirrojo (P): 2 estudiantes.
• Moreno (M): 9 estudiantes.
• Castaño (C): 14 estudiantes.

El conjunto de valores ordenados de una variable estadística se conoce como distribución de frecuencias o serie estadística.

Las frecuencias se clasifican en dos tipos:

A) Frecuencia absoluta:
Indica el número exacto de veces que aparece cada categoría de la variable en estudio. Se representa generalmente como n_i​, donde “n” es el número total de repeticiones y “i” indica la categoría específica de la variable.

En el ejemplo:

• n₁=5 (rubio).
• n₂=2 (pelirrojo).
• n₃=9 (moreno).
• n₄=14 (castaño).

Para verificar que no hay errores, la suma de las frecuencias absolutas debe coincidir con el tamaño total de la muestra (n). En este caso: 5+2+9+14=30.

B) Frecuencia relativa:
Es el cociente entre la frecuencia absoluta de cada categoría y el total de elementos en la muestra o población. Se representa como f_i​, donde “f” es el valor relativo de la categoría “i”.

En el ejemplo:

• f₁=5/30=0,167.
• f₂=2/30=0,066.
• f₃=9/30=0,3.
• f₄=14/30=0,467.

La suma de las frecuencias relativas debe ser igual a 1 (∑ f_i = 1). En este caso: 0,167+0,066+0,3+0,467=1.

Formas adicionales de expresar frecuencias relativas:

1. Porcentajes: Multiplicando la frecuencia relativa por 100 (% = f_i ⋅ 100). En este caso:

• f₁ = 16,7 %.
• f₂ = 6,6 %.
• f₃ = 30 %.
• f₄ = 46,7 %.

Tanto por mil: Multiplicando la frecuencia relativa por 1000 (\permil = f_i ⋅ 1000). Por ejemplo, si la frecuencia relativa de recién nacidos fallecidos es f = 0,15, sería más claro expresarlo como 150 fallecimientos por cada 1000 nacimientos vivos.

Frecuencia acumulada:
Es la suma progresiva de las frecuencias, ya sea absolutas o relativas. Se representa con letras mayúsculas:

• N_i​ para frecuencias acumuladas absolutas.
• F_i​ para frecuencias acumuladas relativas.

En el ejemplo, la frecuencia acumulada absoluta sería:

• N₁ = 5.
• N₂ = 5 + 2 = 7.
• N₃ = 7 + 9 = 16.
• N₄ = 16 + 14 = 30.

Y la frecuencia acumulada relativa:

• F₁ = 0,167.
• F₂ = 0,167 + 0,066 = 0,233.
• F₃ = 0,233 + 0,3 = 0,533.
• F₄ = 0,533 + 0,467 = 1.

Frecuencias Acumuladas y su Uso

Las frecuencias acumuladas se utilizan para organizar los datos de manera que faciliten la localización de valores relevantes como la mediana o los cuantiles. Se pueden distinguir entre:

Frecuencias Acumuladas Absolutas (N):

• Para cualquier valor de la frecuencia acumulada absoluta (N), el cálculo se realiza sumando las frecuencias absolutas (n) desde el inicio hasta el valor deseado.
  • Por ejemplo, para N₁, su valor será igual a n₁ (es decir, 5), ya que no hay ningún valor anterior.
  • Para N₂, será la suma de n₁ + n₂, lo que da 7 (5 + 2).

Frecuencias Acumuladas Relativas (F):

• Representan la proporción acumulada y se calculan sumando las frecuencias relativas (f) hasta el valor deseado.
  • Por ejemplo, para F₁, su valor será igual a f₁ (0,167), ya que no hay valores anteriores.
  • Para F₂, será la suma de f₁ + f₂, lo que da 0,233 (0,167 + 0,066).

Es importante comprobar que:

• La última modalidad de N debe ser igual a n total.
• La última modalidad de F debe ser igual a 1.

Algunos autores utilizan diferentes notaciones para estas medidas:

• n puede aparecer como f (frecuencias absolutas).
• f puede denominarse h (frecuencias relativas).
• N se cambia por F (frecuencias absolutas acumuladas).
• F se cambia por H (frecuencias relativas acumuladas).

Medidas de Frecuencia en Epidemiología

La frecuencia de los fenómenos epidemiológicos puede representarse mediante:

• Números absolutos, que indican cuántas veces ocurre un evento.
• Números relativos, que relacionan dichos eventos con un total o una base de interés.

Es fundamental tener en cuenta que las frecuencias absolutas pueden inducir a errores si no se consideran en relación con el tamaño de la población de donde provienen.

Características a considerar:

• Simplicidad: Los indicadores deben ser fáciles de entender.
• Aceptación: Las poblaciones deben aceptar los estudios realizados.
• Reproducibilidad: Los resultados deben ser consistentes al replicar el estudio.
• Veracidad: Los instrumentos deben medir lo que se pretende analizar.

Principales medidas de frecuencia relativa:

1. Porcentajes:

• Expresan una proporción en términos de 100.
• Ejemplo: Comparar una parte con su totalidad.

2. Razón o Ratio:

• Relaciona dos frecuencias absolutas de variables distintas que no están contenidas una en la otra.
• Ejemplo: Dividir el número de fetos muertos por el de nacidos vivos.

3. Proporción:

• Relaciona dos frecuencias, donde el numerador forma parte del denominador.
• Puede ser:

– Directa: Ambas magnitudes aumentan o disminuyen proporcionalmente.

– Inversa: Una magnitud aumenta mientras la otra disminuye.

4. Tasas:

• Miden la frecuencia de un evento en relación con el tiempo y el tamaño de la población en riesgo.
• Ejemplo: Si en una muestra de 3000 personas durante 3 años hubo 60 casos de una enfermedad, la tasa sería 0,02 por año.

5. Índices:

• Relacionan diferentes valores respecto a uno que se toma como base, asignándole el valor 100.
• Se calculan mediante regla de tres.

6. Riesgos:

• Expresan la probabilidad de que un individuo adquiera una enfermedad durante un estudio.
• Ejemplo: Dividir el número de casos entre el total de individuos en riesgo.

7. Odds y Odds-Ratio:

• El odds es una razón que relaciona la probabilidad de que ocurra un evento frente a que no ocurra.
• Ejemplo: Un odds de 3 indica que por cada 3 personas que sufren el evento, 1 no lo hará.
• El odds-ratio compara los odds entre dos grupos, mostrando la asociación entre dos variables dicotómicas.

Tabulación

La tabulación consiste en resumir y presentar, en forma de tabla, la distribución de frecuencias de una o varias variables de una muestra o población. Esto nos permite obtener una visión general de cómo se distribuyen los datos.

Por ejemplo, si tenemos las calificaciones de un examen en un módulo de un grupo del ciclo superior de documentación sanitaria, las notas individuales no proporcionarían una idea global. Sin embargo, al expresarlas en una tabla donde se indique el número de estudiantes que obtuvieron 10, 9, 8, 7, etc., se facilita el análisis. De manera similar, en un ejemplo de variable cualitativa nominal como el “color del pelo” de los alumnos de un ciclo, podríamos clasificar y tabular los datos según la modalidad y su frecuencia: 5 rubios, 2 pelirrojos, 9 morenos y 14 castaños.

Datos esenciales en una tabla

Las columnas básicas de una tabla incluyen:

1. Primera columna: la variable con sus modalidades.
2. Segunda columna: la distribución de frecuencias absolutas.
3. Tercera columna: la distribución de frecuencias relativas.
4. Cuarta columna: la distribución en porcentajes.
5. Quinta columna: la distribución acumulada de frecuencias absolutas.
6. Sexta columna: la distribución acumulada de frecuencias relativas.

Adicionalmente, pueden agregarse columnas que representen otras distribuciones, como la de marcas de clase, útil para variables cuantitativas continuas en intervalos de clase. La marca de clase corresponde al valor promedio de cada intervalo. En ciertos casos, también se aplica a datos discretos.

Clasificación de tablas de frecuencia

Las tablas de frecuencia se dividen en dos tipos principales:

a) Tablas para variables no agrupadas.

b) Tablas para variables agrupadas.

Tablas de frecuencia para variables no agrupadas

Estas tablas se utilizan principalmente para variables cualitativas y cuantitativas discretas con un rango de variabilidad reducido. Un ejemplo es el caso del atributo “color del pelo” mencionado antes. Estas distribuciones, que no se agrupan, también se conocen como distribuciones de tipo I.

Pasos para construir una tabla de frecuencia:

1. Obtención de datos: Se recogen los datos mediante encuestas o investigaciones relacionadas con el tema.

2. Recuento de frecuencias: Se contabilizan las veces que cada valor de la variable aparece en los datos recopilados.

3. Construcción de la tabla: Con las frecuencias absolutas recopiladas, se calculan las demás frecuencias necesarias y se elabora la tabla.

Elementos de la tabla:

• x: Representa los valores de la variable.
• n: Indica el total de individuos de la muestra.
• nᵢ: Es la frecuencia absoluta de una modalidad, es decir, el número de veces que aparece dicha modalidad (donde i es el índice de la modalidad).
• fᵢ: Es la frecuencia relativa de una modalidad, calculada como el cociente entre la frecuencia absoluta de la modalidad y el total de observaciones (fᵢ = nᵢ / n).
• p: Representa el porcentaje de una modalidad.
• Nᵢ: Corresponde a la frecuencia absoluta acumulada, que es la suma de las frecuencias absolutas de los valores menores o iguales al valor en estudio.
• Fᵢ: Es la frecuencia relativa acumulada, obtenida como la suma de las frecuencias relativas de los valores menores o iguales al valor en estudio.

Otras Columnas y Clasificación de Tablas de Frecuencia

Las tablas de frecuencia pueden incluir columnas adicionales que representen diversas distribuciones. Entre estas, una de las más relevantes es la que muestra la distribución de marcas de clase. Esto es especialmente útil para datos cuantitativos continuos organizados en intervalos de clase, y en algunos casos, también para datos discretos. La marca de clase se define como el valor promedio de cada intervalo.

Clasificación de tablas de frecuencia:

1. Tablas para variables no agrupadas.

2. Tablas para variables agrupadas.

Tablas de Frecuencia para Variables No Agrupadas

Estas tablas se utilizan principalmente para variables cualitativas y cuantitativas discretas con un rango de variabilidad limitado. Un ejemplo es el atributo “color del pelo” mencionado anteriormente. Estas distribuciones también se conocen como distribuciones de tipo I.

Proceso de Construcción:

1. Obtención de datos: Se realiza a través de encuestas o investigaciones relacionadas con el tema.

2. Recuento de frecuencias: Se contabilizan las veces que cada valor de la variable aparece en los datos recopilados.

3. Construcción de la tabla: Con las frecuencias absolutas obtenidas, se calculan las frecuencias relativas, porcentajes y frecuencias acumuladas, completando así la tabla.

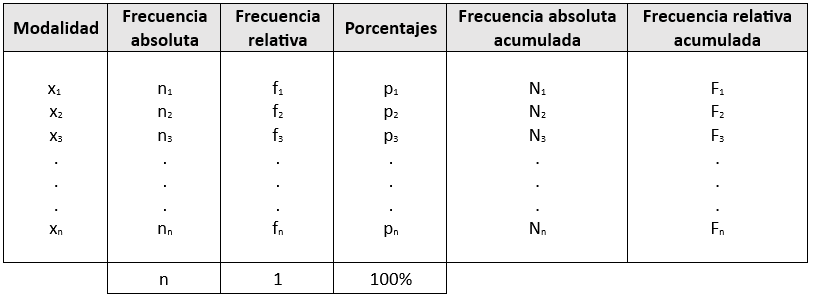
Elementos de la Tabla de Frecuencias:

• x: Representa los valores de la variable.
• n: Es el total de individuos de la muestra.
• nₙ: Es la frecuencia absoluta de una modalidad, es decir, cuántas veces aparece cada valor de la variable. El subíndice i indica el índice de la modalidad.
• fₙ: Es la frecuencia relativa de una modalidad. Se calcula como el cociente entre la frecuencia absoluta de la modalidad y el total de observaciones (fₙ = nₙ / n).
• p: Representa el porcentaje de cada modalidad.
• Nₙ: Es la frecuencia absoluta acumulada, obtenida sumando las frecuencias absolutas de todos los valores menores o iguales al valor en estudio.
• Fₙ: Es la frecuencia relativa acumulada, que se obtiene sumando las frecuencias relativas de todos los valores menores o iguales al valor en estudio.

Con este enfoque, se logra una representación clara y ordenada de los datos, facilitando su análisis y comprensión.

Tablas de Frecuencia para Variables Agrupadas

Las tablas de frecuencia para variables agrupadas son especialmente útiles cuando se trabaja con datos cuantitativos y, en ocasiones, también con datos discretos. Estas tablas se construyen organizando las variables en intervalos de clase, también conocidos como distribuciones de tipo II.

Agrupar valores en intervalos de clase es necesario cuando los datos son continuos, hay muchas modalidades o el tamaño de la muestra es grande. En cada intervalo de clase, se consideran los siguientes elementos:

• Límites de clase: Valores máximo y mínimo del intervalo.
  • Límite superior (Límite_M): Valor máximo.
  • Límite inferior (Límite_m): Valor mínimo.
• Longitud de clase (L): Diferencia entre los límites de clase (Límite_M – Límite_m). Todos los intervalos deben tener la misma longitud, salvo excepciones.
• Marca de clase (X_i): Valor representativo de cada intervalo, calculado como la media aritmética de los límites del intervalo:
• Número de intervalos: Se calcula generalmente como la raíz cuadrada del tamaño muestral.
• Amplitud o rango: Indica la dispersión de los datos, calculándose como la diferencia entre el valor máximo y el valor mínimo:
• Longitud de clase: Aproximadamente igual al cociente entre el rango y el número de intervalos.

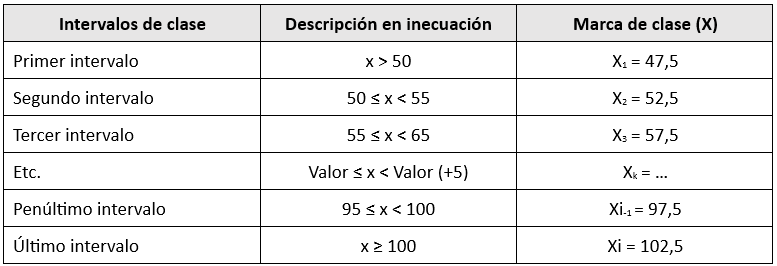
Intervalos Especiales

En algunas situaciones, se crean intervalos que contienen valores extremos de la variable. Estos “intervalos cajón de sastre” no tienen una longitud definida y se expresan como menores o mayores a un valor, por ejemplo, “< X” o “> X”. Las marcas de clase para estos intervalos se calculan de la siguiente manera:

• Primer intervalo: Se resta la longitud de clase al valor de la segunda marca de clase (X₁ = X₂ – L).
• Último intervalo: Se suma la longitud de clase a la penúltima marca de clase (Xₓ = Xₓ₋₁ + L).

Consideraciones para Construir Intervalos de Clase

1. Número de intervalos: Depende del tamaño de la muestra y la dispersión de los datos.

2. Longitud de clase (L): Determinada por el rango y el número de intervalos.

3. No solapamiento: Los intervalos no deben solaparse ni dejar espacios entre ellos.

4. Ajuste de decimales: En variables con decimales, se puede sumar o restar una pequeña fracción para evitar solapamientos. Por ejemplo:

• Límitem inicial: Valor mínimo – 0,04.
• LímiteM final: Valor máximo + 0,04.

Aunque este ajuste introduce un error mínimo, es aceptable para garantizar la correcta tabulación.

Construcción de Tablas de Frecuencia Agrupada

1. Obtención de datos: A través de encuestas o investigaciones.

2. Cálculo del número de intervalos: Utilizando la raíz cuadrada del tamaño muestral.

3. Cálculo de la longitud de clase (L): Dividiendo el rango por el número de intervalos.

4. Ajuste del rango: Evitando solapamientos mediante estrategias como ajustes decimales.

5. Recuento de frecuencias: Determinar cuántos datos pertenecen a cada intervalo.

6. Cálculo de marcas de clase: Sumando los límites superior e inferior de cada intervalo y dividiendo entre dos.

7. Columnas adicionales:

• Marca de clase multiplicada por la frecuencia absoluta (Xₙ × nₙ), para calcular la media aritmética.
• Marca de clase al cuadrado multiplicada por la frecuencia absoluta (Xₙ² × nₙ), para calcular la varianza y la desviación típica.

Ejemplo

Si tenemos las calificaciones de 20 opositores: 4, 7, 6, 5, 3, 6, 8, 3, 5, 6, 7, 6, 6, 4, 5, 6, 5, 5, 4, 3.

La variable “Xi” representa las calificaciones obtenidas, comprendidas entre 3 y 8. Aunque pueden considerarse datos discretos, también podrían tratarse como continuos si se admiten decimales. Estos datos permiten construir una tabla de frecuencia agrupada considerando los intervalos definidos.

Frecuencia Absoluta (fi)

La frecuencia absoluta (fi) representa cuántas veces se repite un valor específico de la variable en un conjunto de datos. Por ejemplo, si únicamente un opositor ha obtenido la puntuación de 8, entonces la frecuencia absoluta asociada a esa puntuación es 1.

La suma de todas las frecuencias absolutas debe coincidir con el número total de datos, denotado como N.

Frecuencia Absoluta Acumulativa (Fi)

La frecuencia absoluta acumulativa (Fi) se calcula sumando la frecuencia absoluta de un valor a las frecuencias absolutas de todos los valores anteriores. Por ejemplo:

F₄ = f₁ + f₂ + f₃ + f₄ = 3 + 3 + 5 + 6 = 17

El último valor de la frecuencia absoluta acumulativa coincide siempre con el número total de datos (N), que en este caso es 20.

Frecuencia Relativa (hi)

La frecuencia relativa (hi) se obtiene dividiendo la frecuencia absoluta de un dato entre el número total de datos (N). Por ejemplo:

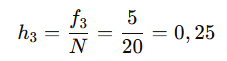
Esto indica que el valor correspondiente al tercer dato representa el 25% del total de datos.

Multiplicando la frecuencia relativa por 100, se obtiene el porcentaje que representa ese valor respecto al total.

La suma de todas las frecuencias relativas es igual a 1.

Frecuencia Relativa Acumulativa (Hi)

La frecuencia relativa acumulativa (Hi) se calcula sumando la frecuencia relativa de un dato a las frecuencias relativas de todos los datos anteriores. Similar a la frecuencia absoluta acumulativa, el último valor de la frecuencia relativa acumulativa será siempre 1.

Cálculo de parámetros estadísticos

Amplitud o Recorrido (R)

La amplitud o recorrido de los datos se calcula como la diferencia entre el valor máximo (X_max) y el valor mínimo (X_min​) de la variable:

R = X_max − X_min

Longitud del Intervalo (L)

La longitud del intervalo se obtiene dividiendo la amplitud entre el número total de intervalos (kkk):L=RkL = \frac{R}{k}L=kR​

Donde kkk es el número de intervalos en los que se agrupan los datos.

Estos conceptos son esenciales para comprender la distribución de los datos y calcular parámetros estadísticos. Para realizar análisis avanzados o cálculos más precisos, se aplicarán las fórmulas descritas, respetando las normas estadísticas correspondientes.

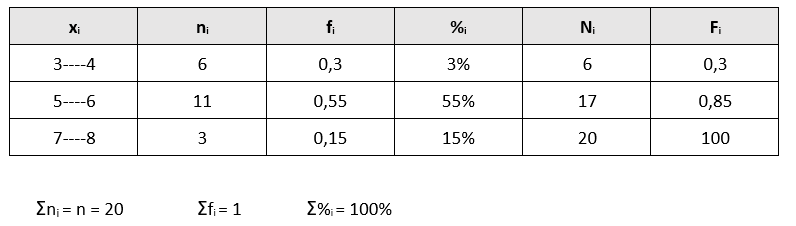
EJEMPLO 2: pretendemos estudiar la estatura de los universitarios (en m) mediante un muestreo de 30 alumnos tomados al azar, y nos da el siguiente resultado:

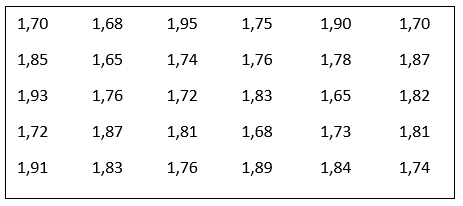
Para calcular parámetros estadísticos, realizamos los siguientes pasos:

a) Amplitud o recorrido (A):

La amplitud o recorrido se define como la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos. En este caso, se calcula de la siguiente manera:

A = X_máx − X_mín = 1.95 − 1.65 = 0.30

b) Longitud del intervalo (L):

La longitud del intervalo se determina dividiendo la amplitud total entre el número de intervalos deseados. Dado que los datos tienen dos decimales, es posible aumentar la precisión añadiendo y restando 0.004, o bien construyendo intervalos mediante inecuaciones, que es el método que utilizaremos.

c) Número de intervalos (k):

Para determinar el número óptimo de intervalos, se puede utilizar el método de la raíz cuadrada del tamaño de la muestra. En este caso, con una muestra de 30 datos, calculamos:

k=n=30≈5.48k = \sqrt{n} = \sqrt{30} \approx 5.48k=n​=30​≈5.48

Redondeando, utilizamos 5 intervalos.

d) Construcción de la tabla y recuento de frecuencias:

Una vez determinados el número de intervalos y su longitud, procedemos a construir una tabla de frecuencias que incluya:

• Intervalos de clase: Definidos según los límites establecidos.
• Frecuencia absoluta (fᵢ): Número de datos que caen dentro de cada intervalo.
• Frecuencia acumulada (Fᵢ): Suma acumulativa de las frecuencias absolutas.
• Frecuencia relativa (hᵢ): Proporción de datos en cada intervalo respecto al total, calculada como h_i = f_i / n
• Frecuencia relativa acumulada (Hᵢ): Suma acumulativa de las frecuencias relativas.

Este proceso nos permite organizar y analizar los datos de manera efectiva, facilitando la interpretación de la distribución y las tendencias presentes en el conjunto de datos.